Trees data structure

A tree data structure is a non-linear data structure because it does not store in a sequential manner. It is a hierarchical structure as elements in a Tree are arranged in multiple levels. In the Tree data structure, the topmost node is known as a root node. Each node contains some data, and data can be of any type.

Properties of Tree

Every tree has a specific root node. A root node can cross each tree node. It is called root, as the tree was the only root. Every child has only one parent, but the parent can have many children.

Common Terminology

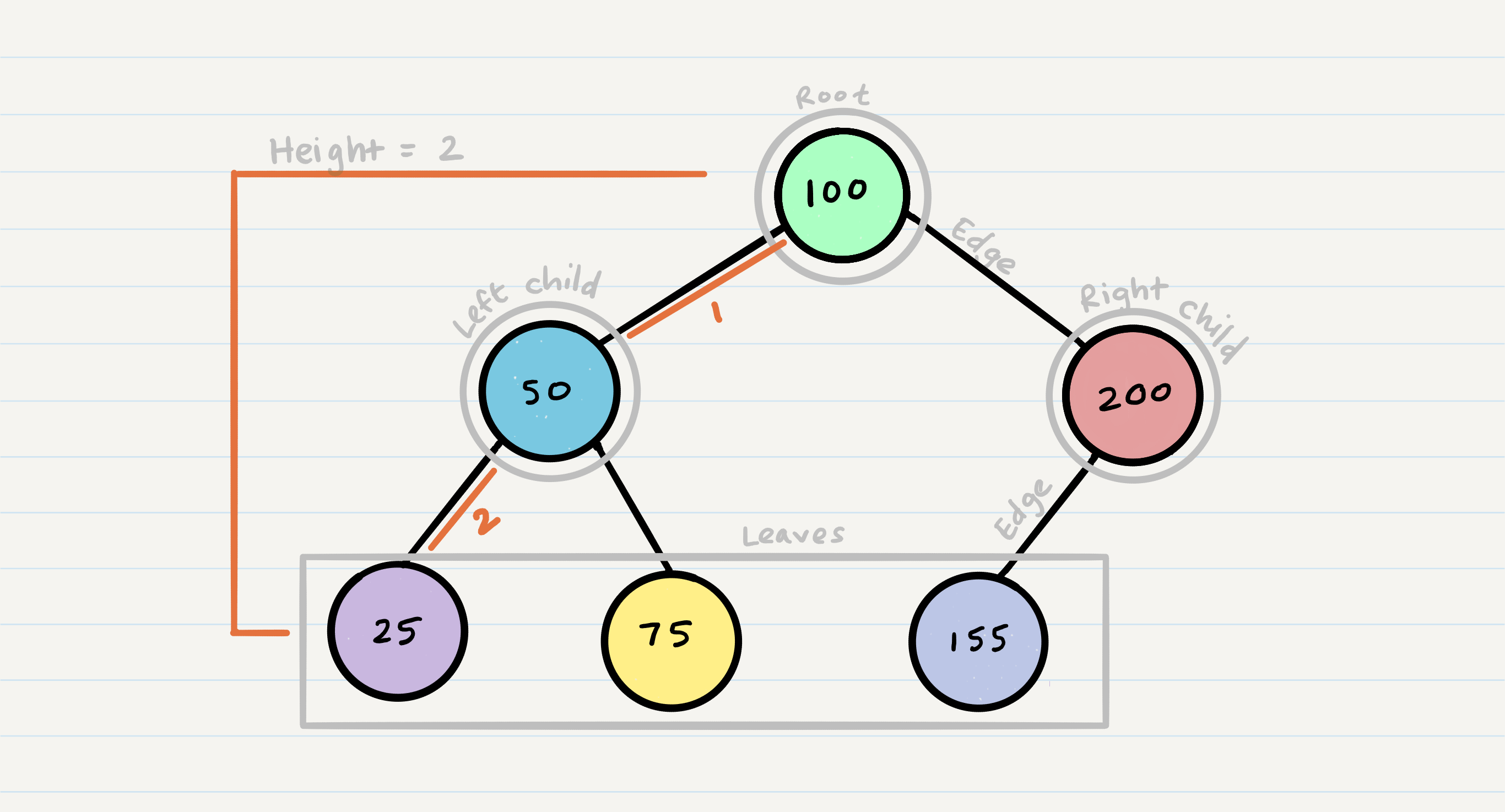
• Node - A Tree node is a component which may contain it’s own values, and references to other nodes
• Root - The root is the node at the beginning of the tree
• K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
• Left - A reference to one child node, in a binary tree
• Right - A reference to the other child node, in a binary tree
• Edge - The edge in a tree is the link between a parent and child node Leaf - A leaf is a node that does not have any children
• Height - The height of a tree is the number of edges from the root to the furthest leaf

Sample Tree

Traversals

1. Depth First : is where we prioritize going through the depth (height) of the tree first

   • methods for depth first traversal: Pre-order: root >> left >> right In-order: left >> root >> right Post-order: left >> right >> root
   • most common way to traverse through a tree is to use recursion

2. Breadth First: iterates through the tree by going through each level of the tree node-by-node.

   • Traditionally, breadth first traversal uses a queue (instead of the call stack via recursion) to traverse the width/breadth of the tree.
   • Dequeue the front node, enqueue that node’s left and right nodes, and move to the next new front of the queue.

Binary Tree Vs K-ary Trees

• Binary Tree: Binary Trees restrict the number of children to two (hence our left and right children).
• K-ary Trees: Nodes are able have more than 2 child nodes
• Breadth First Traversal Traversing a K-ary tree requires a similar approach to the breadth first traversal. We are still pushing nodes into a queue, but we are now moving down a list of children of length k, instead of checking for the presence of a left and a right child.
• adding Node One strategy for adding a new node to a binary tree is to fill all “child” spots from the top down. To do so, we would leverage the use of breadth first traversal. During the traversal, we find the first node that does not have all it’s children filled, and insert the new node as a child. We fill the child slots from left to righ

Binary Search Tree

Binary Search Tree (BST) is a binary tree extension with several optional restrictions. The left child value of a node should in BST be less than or equal to the parent value, and the right child value should always be greater than or equal to the parent’s value. This Binary Search Tree property makes it ideal for search operations since we can accurately determine at each node whether the value is in the left or right sub-tree. This is why the Search Tree is named.